Teorema de Okishio - 5

Quinta parte da tradução e edição de: Okishio's theorem

O modelo em termos físicos

O duplo sistema de equações

Até agora foi só suficiente descrever variáveis monetárias. A fim de expandir a análise para calcular, por exemplo, o valor patrimonial da constante c, o capital variável v e mais-valia (ou lucro) s para a economia como um todo ou para calcular as proporções entre estas figuras como taxa de mais-valia s/v ou composição do valor de capital, é necessário conhecer o tamanho relativo de um departamento em relação a outro. Se ambos os departamentos, I (bens de investimento) e II (bens de consumo) estão crescendo continuamente em equilíbrio deve haver uma certa proporção de tamanho entre estes dois departamentos. Esta proporção pode ser detetada por modelização de crescimento contínuo de nível físico (ou materiais), em oposição ao nível monetário.

Digo e repito: tenho de iniciar uma coleção de charges dos “ditos de esquerda”, boa parte delas incluindo, além de versões ´pictóricas das falácias de costume, uma tendência quase ridícula pelo “rótulo odioso”. - cyberdemocracia.blogspot.com

Nas equações acima, para todos os ramos, uma taxa de lucro geral igual foi calculada dado

• certas condições técnicas descritas por coeficientes de entrada-saída
• um salário real definido por uma determinada cesta de bens de consumo a serem consumidos por hora de trabalho

pelo qual um preço tem de ser arbitrariamente determinado como numerário. Neste caso, o preço 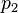para o bem de consumo 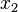sendo definido como igual a 1 (numerário) e o preço para o bem de investimento sendo então calculado. Então, em termos monetários, as condições para um crescimento estável foram estabelecidas.

As equações gerais

Para estabelecer este crescimento estável também em termos do nível de material, o seguinte deve estabelecer-se:

Assim, uma magnitude K adicional deve ser determinada, que descreve a dimensão relativa dos dois ramos I e II em que I tem um peso de 1 e o departamento II tem o peso de K.

Se é assumido que os lucros totais são usados para investimento, a fim de produzir mais no próximo período de produção a nível técnico dado, então a taxa de lucro r é igual à taxa de crescimento g.

Exemplos numéricos

No primeiro exemplo numérico com taxa de lucro 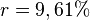tem-se:

O peso do departamento II é .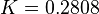

para o segundo exemplo numérico com taxa de lucro tem-se:

Agora, o peso do departamento II é 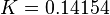. As taxas de crescimento g são iguais as taxas de lucro r, respectivamente.

Para os dois exemplos numéricos, respectivamente, na primeira equação no lado esquerdo, é a entrada e na segunda equação no esquerdo é a quantidade de entrada de 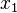e na segunda equação no esquerdo é a quantidade de entrada de . No lado direito das equações dos primeiros dois exemplos numéricos, respectivamente, está a saída de uma unidade de 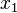e na segunda equação de cada exemplo está a produção de K unidades de.

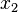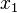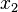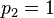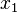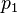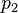A entrada de multiplicada pelo preço resulta o valor monetário de capital constante c. A multiplicação da entrada com o preço definido resulta no valor monetário do capital variável v. Uma unidade de saída e K unidades de saída multiplicada por seus preços e respectivamente resulta nas vendas totais da economia c + v + s.

Subtraindo-se das vendas totais o calor do capital constante adicionado do capital variável (c + v) resulta o lucro s.

Agora a composição de valor do capital c/v, a taxa de mais-valia s/v, e a “parcela salarial” (repartição do valor agregado) v/(s + v) podem ser calculados.

No primeiro exemplo a parcela salarial é 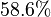e no segundo exemplo 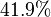. As taxas de mais-valia são, respectivamente, 0.706 e 1.389. A composição de valor de capital c/v é no primeiro exemplo 6,34 e no segundo 12.49. De acordo com a fórmula

Para Latex: \text{Taxa de lucro }p = {{s \over v} \over {{c \over v} + 1}}

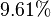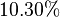para os dois exemplos numéricos as taxas de lucro podem ser calculadas, resultando e , respectivamente. Estas são as mesmas taxas de lucro como foram calculadas diretamente em termos monetários.

Análise comparativa estática

O problema com estes exemplos é que eles se baseiam na estática comparativa. A comparação é entre as diferentes economias cada uma em um caminho de crescimento com equilíbrio. Todos os modelos em desequilíbrio levam a outros resultados. Se os capitalistas levantam a composição técnica do capital, porque, assim, a taxa de lucro é gerada, isso pode levar a um processo contínuo em que a economia não tem tempo o suficiente para chegar a um novo caminho de crescimento em equilíbrio. Há um processo contínuo de aumento da composição técnica do capital em detrimento da criação de emprego resultante, pelo menos no mercado de trabalho em estagnação. A Lei da Queda Tendencial da Taxa de Lucro hoje em dia geralmente é interpretada em termos de análise de desequilíbrio, não menos importante em reação à crítica de Okishio.